Tag: statistic

If you need a reminder on how the Hill Cipher works click here.

The first thing to note is that when encoding in Hill Cipher each row of the key matrix encodes to 1 letter independently of the rest of the key matrix.

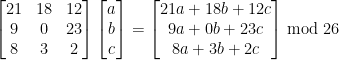
Notice how the top row of the far left matrix is only involved in the top cell of the ciphertext matrix, the middle row is only involved in the middle cell etc.

We can use this fact to dramatically decrease the number of keys we have to test to break the Hill Cipher.

For square matrix of size N, there are 26^N×N unique keys (there will be less as not all matrices have an inverse). For N=3, there is 26⁹ ≈ 5.43×10¹² keys, to test all of these is not feasible (I calculated on my pc it would take ≈ 8 years to test them all).

However, if we test each row individually then there is only 26^N keys we need to test, For N=3 there is 26³ = 17,576 which is a very small number in comparison (Takes 0.5 seconds on my pc!)

With this property of Hill Cipher we can go about cracking it.

First you will need to identify N (the size of the matrix) the size will be a multiple of the text length – this narrows it down a lot

Now you will be to iterate over all the row vectors with a size of N and possible values of 0 (inclusive) to 26 (exclusive).

For a 3 by 3 there are 17,576 combinations. They look will look something like this. On the left is the iteration number…

1/17576         [ 0,  0,  0]
2/17576         [ 0,  0,  1]
3/17576         [ 0,  0,  2] ……
16249/17576     [24,  0, 24]
16250/17576     [24,  0, 25]
16251/17576     [24,  1,  0] ……
17576/17576     [25, 25, 25]

For each one of these possibilities assume it is part of the key and multiply your ciphertext by it, you will multiply in blocks of N and get a single letter out for each block.

Once you have all the output letters for a particular possibility, score the letters using the Chi-Squared Statistic. Store the row vectors from smallest to largest Chi-Squared value.

Once you have checked all the possibilities. Take the best results from the list you have compiled and then go through all the permutations of creating an N by N matrix and checking it has an inverse in modular 26.

Example:

Let’s say you know N=3 and the best row vectors found using this method were with a Chi-Squared value of… (note is some cases the best N vectors may not be the correct ones so you may need to try a combination of a few different ones)

[22,  6,  7]    X² = 71.721647
[23, 17, 18]    X² = 50.562860
[25,  0,  6]    X² = 81.987751

Rearranging each row to every possible position (For R number of rows there is R!, R×(R-1)×(R-2)…×1, permutations)

The next (3! = 6) matrices are all the permutations of each row vector.

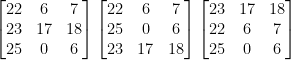
Then encrypt your ciphertext using these matrices (encrypting using the inverse key matrix is the same as decrypting using the key matrix). One of these results should be English – being your solution. If you wish to find the key matrix, you will need to inverse the inverse key matrix in mod 26.

To Conclude

For larger matrices like 4 by 4 and up the sheer number of keys make a brute force attack impossible, I don’t believe anyone has the patience or life expectancy to wait around 64 trillion years to solve one cipher. Other methods like crib dragging require you to guess or make assumptions for large chunks of the plaintext, a crib of 19+ characters very hard to come by. The method described above can solve a 4 by 4 Hill cipher in about 10 seconds, with no known cribs. The only thing it requires is that the text is of a certain length, about 100×(N-1) or greater when N is the size of the matrix being tested, so that statistical properties are not affected by a lack of data.

This same method can be adapted to decrypted ciphertext in other languages you just need to change the frequencies of letters that the Chi-Squared Statistic uses.

[powr-hit-counter id=4db2581c_1482002480525]