Caesar Cipher

The Caesar Cipher is one of the most commonly used and simplest ciphers, named after Julius Caesar, it is a great place to start learning about ciphers.

Encryption

The key is an integer normally known as the ‘shift’, it can be a number from 0-25 (0 being the identity). First you create your alphabet mapping of plaintext letters (lowercase) to ciphertext letters (uppercase) using the shift.

Some examples a shifts would look like this

Shift of 1:                Shift of 21:
abcdefghijklmnopqrstuvwxyz abcdefghijklmnopqrstuvwxyz
BCDEFGHIJKLMNOPQRSTUVWXYZA VWXYZABCDEFGHIJKLMNOPQRSTU

For each letter in your plaintext you replace it it with its corresponding ciphertext letter (the one below it in the mapping).

It can also be thought of like converting each letter to is equivalent value (A=0, B=1…. Z=25 etc) and adding the key shift, and subtracting 26 if the value is 26 or greater, then convert back to letters.

Example:

Encrypting “when the clock strikes twelve attack” using the shift of 21

when the clock strikes twelve attack
RCZI OCZ XGJXF NOMDFZN ORZGQZ VOOVXF

Decryption

For each letter in your ciphertext you replace it it with its corresponding plaintext letter (the one above it in the mapping).

You can also convert each letter to is equivalent value (A=0, B=1…. Z=25 etc) and subtract the key shift this time, and add 26 if the value smaller than 0, then convert back to letters.

VWXYZABCDEFGHIJKLMNOPQRSTU - Shift of 21:
abcdefghijklmnopqrstuvwxyz 

RCZI OCZ XGJXF NOMDFZN ORZGQZ VOOVXF
when the clock strikes twelve attack

As we are working in modular 26 a shift of -5 is the same as a shift of 21. The inverse key of 21 would be 5.

New: Try it yourself!

Cryptanalysis of the Nihilist Substitution Cipher

If you need a reminder on how the Nihilist Substitution Cipher works click here.

To find the period you assume it is a particular period and put in blocks of 2 in columns of the period, then you do an diagraphic index of coincidence calculation on each column and take the average of all the columns.

This is an example of the difference between the expected English index of coincidence (0.0667) and the average Index of Coincidence Calculation for periods 2-40. Hence the smaller the bar the closer it is to that of English.

Average Index of Coincidence values for periods 2-40

As you can see for this particular text it is very obvious that the period is 3 because all the of multiples of 3s are very close to English. This is because the key ‘MAN’ – period 3 is the same as ‘MANMAN’ – period 6.

Once the period has been identified place the ciphertext into blocks of 2 in columns of the correct period.

Example:
345173345643531536543672… has been found to have a period of 3

?  ?  ?  = Key
34 51 73
34 56 43
53 15 36
54 36 72
........

From this point on you treat each column separately as they are all encoded by a different letter. From here we use each number digraph to narrow down the possible keys. We can infer things from ciphertext for example if the second digit is 0 there was only one way it could have been created that would be the plaintext number and the key number ending in a 5.

This can be extended to create inequalities for all possible ciphertext number digraphs. This is some pseudocode to create an inequalities for both the row and column.

rowMin = 1
rowMax = 5
colMin = 1
colMax = 5
no = ciphertext number digraph

IF no is smaller than 11 THEN
    no = no + 100

col = no % 10
IF col equals 0 THEN
    colMin = 5
    colMax = 5
    no = no - 10
ELIF col smaller than 7 THEN
    colMin = 1
    colMax = col - 1
ELSE
    colMin = col - 5
    colMax = 5

row = floor(no / 10) % 10

IF row equals 0 THEN
    rowMin = 5
    rowMax = 5
ELIF row smaller than 7 THEN
    rowMin = 1
    rowMax = row - 1
ELSE
    rowMin = row - 5
    rowMax = 5

You apply this algorithm to all number digraphs in each column and then create an equation for the row and column of the key number. The equation will be…

rowMin <= row <= rowMax
colMin <= col <= colMax

You then use these to narrow down the possibility, lets say you had the inequalities …

2 <= row <= 4  &  3 <= row <= 5  &  2 <= row <= 3

From these three inequalities you can infer that:

3 <= row <= 3 hence row = 3

So you now know that for that columns the key number must starts with a 3. You can then get the inequalities for the column and then create the full key which in this case will now be 31, 32, 33, 34 or 35.

Once the key has been found for each column subtract it away from each number in its respective column. Now if there have been no mistakes there should be less than 25 (size of polybius square with I/J being 1 character) number digraphs. Convert each unique one into a unique letter. Example: swap out all 24 for ‘A’s all 45 for ‘B’s, all 86 for ‘C’s etc.

You are now left will a simple substitution cipher, I wont go into detail on how to break it here, but I have a page here on how to break a simple substitution cipher. Tips: The most common letter in the new ciphertext will likely be ‘E’, the most common trigraph ‘THE’ and so on.

Nihilist Substitution Cipher

The Nihilist Substitution is a poly-alphabetic cipher which means it uses multiple substitution alphabets and similar to the Vigenère Cipher.

The key consists of a 5×5 polybius square which has all the letters in the alphabet however I/J are treated the same and a second key.

	1	2	3	4	5
1	A	B	C	D	E
2	F	G	H	I/J	K
3	L	M	N	O	P
4	Q	R	S	T	U
5	V	W	X	Y	Z

The second key can be of any length, keep in mind that the longer the key the more secure it theoretically is, however the key should be memorable so a person could remember and use it. Examples:

MAGIC, KEY, DEFEND, POLYALPHABETIC etc.

Encryption

Consider the polybius square created using the keyword CIPHER

	1	2	3	4	5
1	C	I/J	P	H	E
2	R	A	B	D	F
3	G	K	L	M	N
4	O	Q	S	T	U
5	V	W	X	Y	Z

and a second key of PAGE which defines the period as 4.

The second key is replaced with its position the polybius square (row then column), the numbers effectively become the key. Then each plaintext letter is written in rows of the period length and it too also replaced with its position the polybius square (row then column). The cipher text is then the sum of the key and the cipher text numbers. If the number is greater than 99 (3 digit number) subtract 100. 105 becomes 05, 100 becomes 00.

P  A  G  E   P  A  G  E   P  A  G  E
13 22 31 15  13 22 31 15  13 22 31 15
-----------  -----------  -----------
W  H  E  N   S  T  R  I   E  A  T  T
52 14 15 35  43 44 21 12  15 22 44 44
65 36 46 50  56 66 52 27  28 44 75 59
-----------  -----------  -----------
T  H  E  C   K  E  S  T   A  C  K
44 14 15 11  32 15 43 44  22 11 32
57 36 46 26  45 37 74 59  35 33 63
-----------  -----------
L  O  C  K   W  E  L  V 
33 41 11 32  52 15 33 51
46 63 42 47  65 37 64 66

WHENTHECLOCKSTRIKESTWELVEATTACK using these keys encrypts to 65364650573646264663424756665227453774596537646628447559353363.

Decryption

To decrypt simply split the number text into blocks of 2 and write each block in rows of the period length then subtract the key numbers. If the result is less than 0 add 100.

There are however some serious flaws that significantly decrease the security of this cipher, these flaws can be used to break the Nihilist Substitution Cipher.

New: Try it yourself!

Cryptanalysis of Hill Cipher

If you need a reminder on how the Hill Cipher works click here.

The first thing to note is that when encoding in Hill Cipher each row of the key matrix encodes to 1 letter independently of the rest of the key matrix.

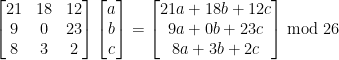
$\begin{bmatrix}21 & 18 & 12 \\9 & 0 & 23 \\8 & 3 & 2 \end{bmatrix}\begin{bmatrix}a \\b \\c \end{bmatrix}=\begin{bmatrix}21a+18b+12 c \\9 a+0b+23c \\8a+3b+2c \end{bmatrix}\bmod 26$

Notice how the top row of the far left matrix is only involved in the top cell of the ciphertext matrix, the middle row is only involved in the middle cell etc.

We can use this fact to dramatically decrease the number of keys we have to test to break the Hill Cipher.

For square matrix of size N, there are 26^N×N unique keys (there will be less as not all matrices have an inverse). For N=3, there is 26⁹ ≈ 5.43×10¹² keys, to test all of these is not feasible (I calculated on my pc it would take ≈ 8 years to test them all).

However, if we test each row individually then there is only 26^N keys we need to test, For N=3 there is 26³ = 17,576 which is a very small number in comparison (Takes 0.5 seconds on my pc!)

With this property of Hill Cipher we can go about cracking it.

First you will need to identify N (the size of the matrix) the size will be a multiple of the text length – this narrows it down a lot

Now you will be to iterate over all the row vectors with a size of N and possible values of 0 (inclusive) to 26 (exclusive).

For a 3 by 3 there are 17,576 combinations. They look will look something like this. On the left is the iteration number…

1/17576         [ 0, 0, 0]
2/17576         [ 0, 0, 1]
3/17576         [ 0, 0, 2] ……
16249/17576     [24, 0, 24]
16250/17576     [24, 0, 25]
16251/17576     [24, 1, 0] ……
17576/17576     [25, 25, 25]

For each one of these possibilities assume it is part of the key and multiply your ciphertext by it, you will multiply in blocks of N and get a single letter out for each block.

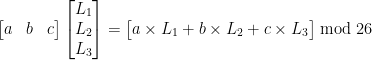
$\begin{bmatrix}a & b & c \end{bmatrix} \begin{bmatrix}L_{1} \\L_{2} \\L_{3} \end{bmatrix}=\begin{bmatrix}a\times L_{1} + b\times L_{2} + c\times L_{3} \end{bmatrix}\bmod26$

Once you have all the output letters for a particular possibility, score the letters using the Chi-Squared Statistic. Store the row vectors from smallest to largest Chi-Squared value.

Once you have checked all the possibilities. Take the best results from the list you have compiled and then go through all the permutations of creating an N by N matrix and checking it has an inverse in modular 26.

Example:

Let’s say you know N=3 and the best row vectors found using this method were with a Chi-Squared value of… (note is some cases the best N vectors may not be the correct ones so you may need to try a combination of a few different ones)

[22, 6, 7]    X² = 71.721647
[23, 17, 18]    X² = 50.562860
[25, 0, 6]    X² = 81.987751

Rearranging each row to every possible position (For R number of rows there is R!, R×(R-1)×(R-2)…×1, permutations)

The next (3! = 6) matrices are all the permutations of each row vector.

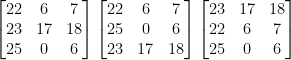
$\begin{bmatrix}22 & 6 & 7 \\23 & 17 & 18\\25 & 0 & 6 \end{bmatrix} \begin{bmatrix}22 & 6 & 7 \\25 & 0 & 6\\23 & 17 & 18 \end{bmatrix} \begin{bmatrix}23 & 17 & 18 \\22 & 6 & 7\\25 & 0 & 6\end{bmatrix}$
$\begin{bmatrix}25 & 0 & 6 \\22 & 6 & 7\\23 & 17 & 18 \end{bmatrix}\begin{bmatrix}25 & 0 & 6 \\23 & 17 & 18\\22 & 6 & 7 \end{bmatrix}\begin{bmatrix}{23} & 17 & 18 \\25 & 0 & 6\\22 & 6 & 7\end{bmatrix}$

Then encrypt your ciphertext using these matrices (encrypting using the inverse key matrix is the same as decrypting using the key matrix). One of these results should be English – being your solution. If you wish to find the key matrix, you will need to inverse the inverse key matrix in mod 26.

To Conclude

For larger matrices like 4 by 4 and up the sheer number of keys make a brute force attack impossible, I don’t believe anyone has the patience or life expectancy to wait around 64 trillion years to solve one cipher. Other methods like crib dragging require you to guess or make assumptions for large chunks of the plaintext, a crib of 19+ characters very hard to come by. The method described above can solve a 4 by 4 Hill cipher in about 10 seconds, with no known cribs. The only thing it requires is that the text is of a certain length, about 100×(N-1) or greater when N is the size of the matrix being tested, so that statistical properties are not affected by a lack of data.

This same method can be adapted to decrypted ciphertext in other languages you just need to change the frequencies of letters that the Chi-Squared Statistic uses.

[powr-hit-counter id=4db2581c_1482002480525]

Hill Cipher

Encryption

To encrypt in Hill a key first needs to be chosen, this will be a square matrix which has an inverse in modular 26. For the matrix to have an inverse the determinant must be co-prime to 26.

Here are two example matrices…
$M_{2}=\begin{bmatrix}2 & 3 \\5 & 3 \end{bmatrix}, M_{3}=\begin{bmatrix}25 & 2 & 11 \\19 & 5 & 12 \\21 & 22 & 6 \end{bmatrix}$
$det(M_{2})=-9$ (-9 mod 26) is 17 (-9+26×1), 17 is co-prime to 26
$det(M_{3})=-2131$ (-2131 mod 26) is 1 (-2131+26×82), 1 is co-prime to 26
Hence both these matrices are valid keys for the Hill cipher
*Co-prime means that the greatest common factor between the two numbers is 1.

If a 2 by 2 matrix is chosen for the key, the plaintext must be padded usually with an ‘X’ so that it is a multiple of 2. So for an N by N matrix the plaintext must be padded so that it that it is a multiple of N. E.G
For N=2, “CAREFUL” would become “CAREFULX”
For N=2, “SPORTS” would stay as “SPORTS”
For N=3, “CAREFUL” would become “CAREFULXX”
Once the text is a valid length, you take letters in blocks of N and convert them to a column vector. Letter ‘A’ has the value 0, ‘B’ is 1, ‘C’ is 2 … ‘Z’ is 25 etc.

Example:
$CA=\begin{bmatrix}2 \\0 \end{bmatrix}$ , $RE=\begin{bmatrix}17 \\4 \end{bmatrix}$ , $FU=\begin{bmatrix}5 \\20 \end{bmatrix}$ , $LX=\begin{bmatrix}11 \\23 \end{bmatrix}$
$CAR=\begin{bmatrix}2 \\0 \\17 \end{bmatrix}$ , $EFU=\begin{bmatrix}4 \\5 \\20 \end{bmatrix}$ , $LXX=\begin{bmatrix}11 \\23 \\23 \end{bmatrix}$

You do this for each block of N characters. Then multiply the key matrix by each column vector. You will get a new column vector which can be converted back to letters.

$\begin{bmatrix}2&3 \\5&3 \end{bmatrix}\begin{bmatrix}2 \\0 \end{bmatrix}=\begin{bmatrix}2\times2+3\times0 \\5\times2+3\times0 \end{bmatrix}=\begin{bmatrix}4 \\10 \end{bmatrix}\bmod26$
“CAREFUL” encodes to “EKUTSHNU” using the key matrix M₂

$\begin{bmatrix}25 & 2 & 11 \\19 & 5 & 12 \\21 & 22 & 6 \end{bmatrix}\begin{bmatrix}2 \\0 \\17 \end{bmatrix}=\begin{bmatrix}25\times2+2\times0+11\times17 \\19\times2+5\times0+12\times17 \\21\times2+22\times0+6\times17 \end{bmatrix}=\begin{bmatrix}3 \\8 \\14 \end{bmatrix}\bmod26$
“CAREFULX” encodes to “DIOSDCCCR” using the key matrix M₃