Tag: polyalphabetic

Cryptanalysis of the Nihilist Substitution Cipher

If you need a reminder on how the Nihilist Substitution Cipher works click here.

To find the period you assume it is a particular period and put in blocks of 2 in columns of the period, then you do an diagraphic index of coincidence calculation on each column and take the average of all the columns.

This is an example of the difference between the expected English index of coincidence (0.0667) and the average Index of Coincidence Calculation for periods 2-40. Hence the smaller the bar the closer it is to that of English.

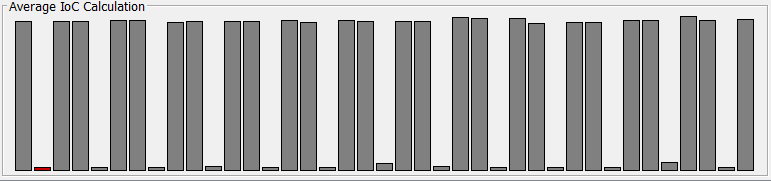
Average Index of Coincidence values for periods 2-40

As you can see for this particular text it is very obvious that the period is 3 because all the of multiples of 3s are very close to English. This is because the key ‘MAN’ – period 3 is the same as ‘MANMAN’ – period 6.

Once the period has been identified place the ciphertext into blocks of 2 in columns of the correct period.

Example:
345173345643531536543672… has been found to have a period of 3

?  ?  ?  = Key
34 51 73
34 56 43
53 15 36
54 36 72
........

From this point on you treat each column separately as they are all encoded by a different letter.  From here we use each number digraph to narrow down the possible keys. We can infer things from ciphertext for example if the second digit is 0 there was only one way it could have been created that would be the plaintext number and the key number ending in a 5.

This can be extended to create inequalities for all possible ciphertext number digraphs. This is some pseudocode to create an inequalities for both the row and column.

rowMin = 1
rowMax = 5
colMin = 1
colMax = 5
no = ciphertext number digraph

IF no is smaller than 11 THEN
    no = no + 100

col = no % 10
IF col equals 0 THEN
    colMin = 5
    colMax = 5
    no = no - 10
ELIF col smaller than 7 THEN
    colMin = 1
    colMax = col - 1
ELSE
    colMin = col - 5
    colMax = 5

row = floor(no / 10) % 10

IF row equals 0 THEN
    rowMin = 5
    rowMax = 5
ELIF row smaller than 7 THEN
    rowMin = 1
    rowMax = row - 1
ELSE
    rowMin = row - 5
    rowMax = 5

You apply this algorithm to all number digraphs in each column and then create an equation for the row and column of the key number. The equation will be…

rowMin <= row <= rowMax
colMin <= col <= colMax

You then use these to narrow down the possibility, lets say you had the inequalities …

2 <= row <= 4  &  3 <= row <= 5  &  2 <= row <= 3

From these three inequalities you can infer that:

3 <= row <= 3 hence row = 3

So you now know that for that columns the key number must starts with a 3. You can then get the inequalities for the column and then create the full key which in this case will now be 31, 32, 33, 34 or 35.

Once the key has been found for each column subtract it away from each number in its respective column. Now if there have been no mistakes there should be less than 25 (size of polybius square with I/J being 1 character) number digraphs. Convert each unique one into a unique letter. Example: swap out all 24 for ‘A’s all 45 for ‘B’s, all 86 for ‘C’s etc.

You are now left will a simple substitution cipher, I wont go into detail on how to break it here, but I have a page here on how to break a simple substitution cipher. Tips: The most common letter in the new ciphertext will likely be ‘E’, the most common trigraph ‘THE’ and so on.

Nihilist Substitution Cipher

The Nihilist Substitution is a poly-alphabetic cipher which means it uses multiple substitution alphabets and similar to the Vigenère Cipher.

The key consists of a 5×5 polybius square which has all the letters in the alphabet however I/J are treated the same and a second key.

  1 2 3 4 5
1 A B C D E
2 F G H I/J K
3 L M N O P
4 Q R S T U
5 V W X Y Z

The second key can be of any length, keep in mind that the longer the key the more secure it theoretically is, however the key should be memorable so a person could remember and use it. Examples:

MAGIC, KEY, DEFEND, POLYALPHABETIC etc.

Encryption

Consider the polybius square created using the keyword CIPHER

  1 2 3 4 5
1 C I/J P H E
2 R A B D F
3 G K L M N
4 O Q S T U
5 V W X Y Z

and a second key of PAGE which defines the period as 4.

The second key is replaced with its position the polybius square (row then column), the numbers effectively become the key. Then each plaintext letter is  written in rows of the period length and it too also replaced with its position the polybius square (row then column). The cipher text is then the sum of the key and the cipher text numbers. If the number is greater than 99 (3 digit number) subtract 100. 105 becomes 05, 100 becomes 00.

P  A  G  E   P  A  G  E   P  A  G  E
13 22 31 15  13 22 31 15  13 22 31 15
-----------  -----------  -----------
W  H  E  N   S  T  R  I   E  A  T  T
52 14 15 35  43 44 21 12  15 22 44 44
65 36 46 50  56 66 52 27  28 44 75 59
-----------  -----------  -----------
T  H  E  C   K  E  S  T   A  C  K
44 14 15 11  32 15 43 44  22 11 32
57 36 46 26  45 37 74 59  35 33 63
-----------  -----------
L  O  C  K   W  E  L  V 
33 41 11 32  52 15 33 51
46 63 42 47  65 37 64 66

WHENTHECLOCKSTRIKESTWELVEATTACK using these keys encrypts to 65364650573646264663424756665227453774596537646628447559353363.

Decryption

To decrypt simply split the number text into blocks of 2 and write each block in rows of the period length then subtract the key numbers. If the result is less than 0 add 100.

There are however some serious flaws that significantly decrease the security of this cipher, these flaws can be used to break the Nihilist Substitution Cipher.

New: Try it yourself!